特值法是行测数量关系中常用的一种方法,通过将一些未知量设成特殊值,从而简化运算过程,快速解决问题。比如工程问题、行程问题、利润问题等均会用到这个方法。但实际上行测中还有一类必考的题目也可以用特值法,那就是几何问题。通过设特值可以将不规则图形变为规则图形,将动点变成特殊点,从而快速得到答案。
下面就几何中的动点问题,为各位考生讲解如何用特值来解决此类问题。

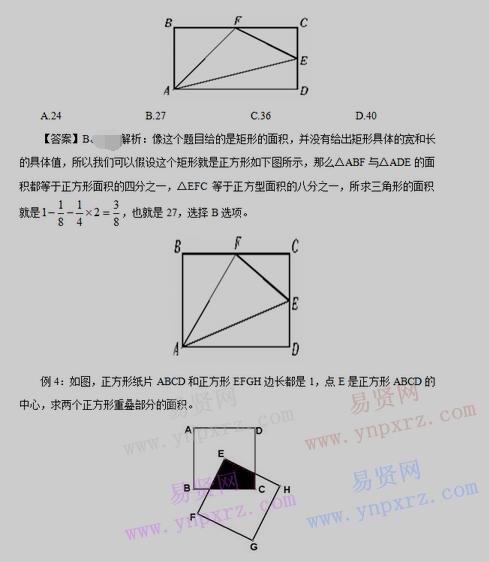
解析:让正方形EFGH绕着点E逆时针旋转,当旋转到EF和BC垂直的时候,两个正方形的重叠部分正好是一个小的正方形,其边长为正方形ABCD的一半,所以面积为正方形ABCD的四分之一,即所求面积为四分之一。
特值思想不仅施设未知量为一个特殊值,也可以把几何中的某一点放到特殊位置,以达到快速求解的目的。通过以上题目的分析,希望广大考生有所启发,在后期的备考中针对性备考,提高学习效率。

